백준 2133번 - 타일 채우기 (Java)

https://www.acmicpc.net/problem/2133

 

 

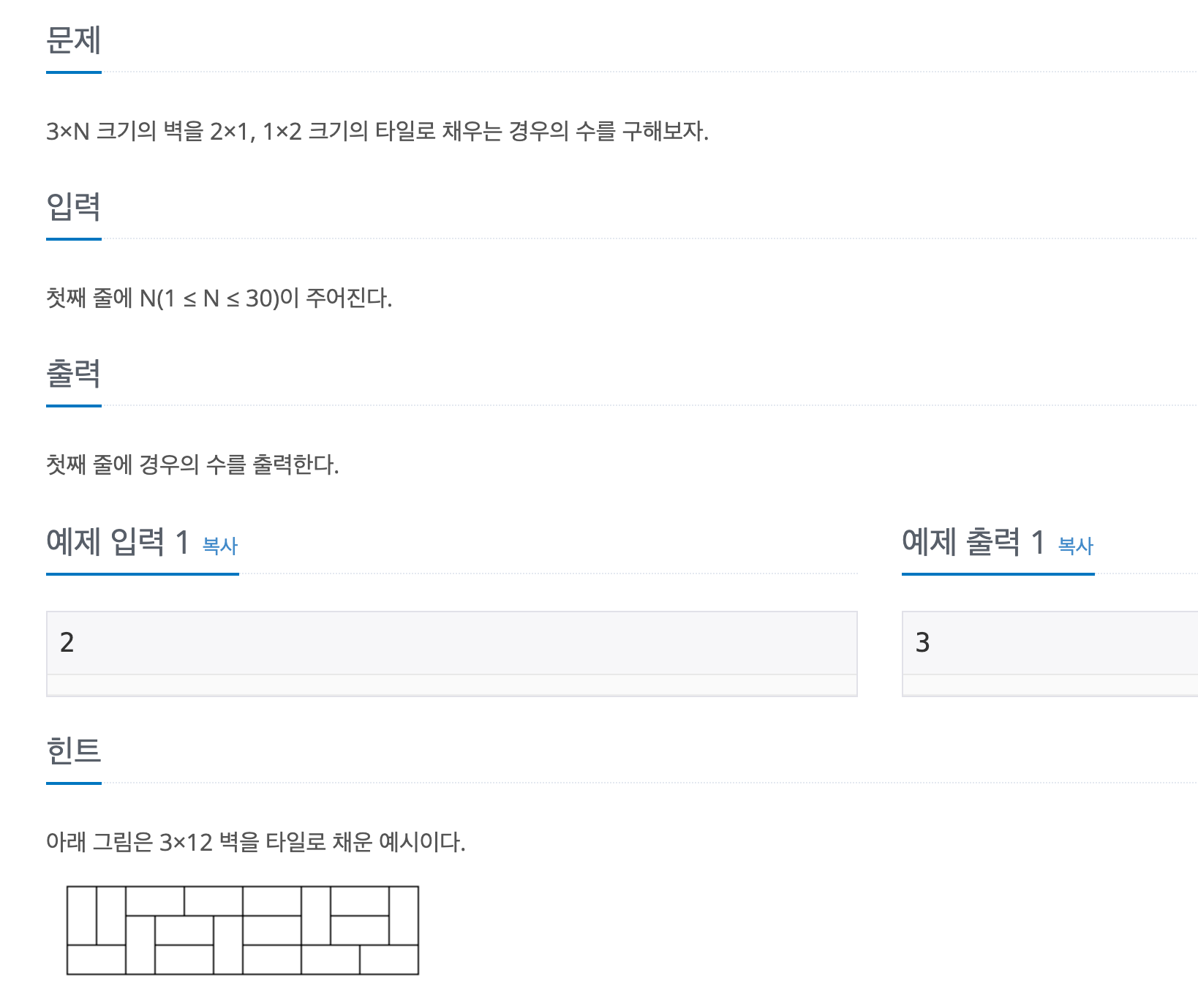
타일 채우기 문제이다. 

 

3xN 크기의 벽을 2x1, 1x2 크기의 타일로 채우는 경우의 수를 구하는 문제니까 

일단, 3x1크기의 벽에 2x1, 1x2 크기의 타일을 넣어보자

제일 왼쪽의 3 x 1의 타일에 1 x 2와 2 x 1의 타일은 넣을 수가 없다. 무조건 한 칸이 남는다. 

3 x 3, 3 x 5 .. 등 홀수 크기의 벽은 채울 수가 없다.

 

그럼 짝수인 3 x 2의 경우의 수는 몇 개일까?

2 x 1 타일과 1 x 2타일로 만들 수 있는 경우의 수는 총 3개다. 

dp[]라는 배열로 문제를 해결할 때 N이 2일 때는 3개인 것이다. 즉 dp[2] = 3이다.

 

3 x 3은 홀수니까 패스하고 

 

3 x 4는 몇 개 일까? 어떻게 구할까? 

dp[2]의 3가지 경우에 A, B, C 타일이 각각 3번씩 사용되면서 총 9번의 경우의 수가 발생된다. 

하지만 이게 끝이 아니다. 2가지가 더 존재한다. 어떤 경우냐면 

이 2개의 특별한 타일의 수도 포함해야 한다. 그리고 이 두 타일은 앞으로 계속 발생한다. 

노란색으로 색칠한 부분은 N이 증가할수록 같이 증가한다.

즉, 3x4 일 때, 3x6 일 때, 3x8일 때... 3 x N일 때 .. 계속 2번씩'만' 발생한다. 

그러니까 앞으로 계산할 3 X N 경우의 수에 2는 계속 더해줘야 한다는 말이다.

 

따라서 3 x 4 타일일 때 경우의 수는 11번(9+2)이다. 

 

그럼 이제 3 x 6도 구해보자. 

위와 같이 두 경우로 나눠볼 수 있다. dp[2]를 우측에 붙여주는 경우부터 보자

아까 3 x 4일 때 11이라는 경우의 수를 구했다. 그 11가지 경우의 수에 A, B, C 타일을 각각 우측에 붙여주면 

3x6의 경우의 수를 구할 수 있다. 오른쪽 그림의 타일들은 dp[2] = 3 일 때의 타일들이다. 

 

3 x 6의 예시를 그려보자면

3 x 4타일에 A타일만 우측에 붙인 경우인데, B타일과 C타일도 다 붙인 경우의 수는

dp[4](11가지) x 3(A, B, C타일) = 33가지다.  dp[2]가 3가지 경우니까 dp[4] x dp[2]로 표현해도 된다. 

현재까지 구한 33가지는 dp[4]에 dp[2]를 우측에 붙였을 때 경우의 타일들만 곱한 경우고 

dp[4]에 dp[2]를 좌측에 붙였을 때의 경우도 구해주어야 한다. 단순히 우측에 붙였던 타일들을 

좌측에만 붙인다고 생각해 보자. 그럼 기존 33가지에 추가 33 가지 해서 66가지 일까? 아니다.

특별한 타일에 dp[2]를 붙이는 경우를 제외한 나머지 경우는 모두 중복이다.

따라서 중복을 제외하면 dp[4]에 dp[2]를 좌측에 붙이는 경우는 

dp[4]의 특별한 타일에 dp[2]의 타일들을 각각 붙여주는 경우 6가지뿐이다.

(2가지(특별한 타일) x 3(A, B, C타일))

 

추가로 dp[6]일 때 특별한 타일의 수 2가지도 더해줘야 한다. (+2)

즉, 3 x 6 타일의 경우의 수는 33 + 6 + 2 = 41이다. 

 

정리해 보면

 

짝수만큼 N이 증가함에 따라

1. 이전에 구한 경우의 수(N-2)에 3가지 타일(dp[2])을 붙이는 경우의 수

2. 특별한 타일의 수(2가지)에 3가지 타일(dp[2])이 붙는 경우의 수 

-> 특별한 타일에 붙이는 것 말고는 모두 중복이다.

3. N일 때 생기는 특별한 경우의 수 2가지는 매번 더해준다. 

 

지금까지 과정을 그림으로 보면 아래와 같이 나타낼 수 있다.

 

3 x 8인 경우도 구해보자. 3 x 8은 3 x 6과 다르게 dp[4] x dp[4] 모양도 가능하다.

1. dp[6] 타일 우측에 dp[2]의 3가지 타일을 붙이는 경우 (41 x 3 = 123) 

2. dp[6] 타일 좌측에 dp[2]의 3가지 타일을 붙이는 경우 즉, 

특별한 타일의 수 (2가지)에 3가지 타일(dp[2])이 붙는 경우의 수 (2 x 3 = 6)

3. 1,2번과의 중복을 피하면서 타일을 채우는 경우는 dp[4]의 특별한 타일을 이용하는 것 말고는 없다.

따라서, 11 x 2 = 22가지이다.

4. dp[8] 일 때 발생하는 특별한 타일의 수 2가지 

 

1,2,3,4를 모두 더하면 123 + 6 + 22 + 2 = 153이다.

 

지금까지 구한 내용들을 코드로 작성해 보자.

0. N이 홀수 일 때는 0을 출력하고 return 한다. 

1. dp[N]일 때 dp[N-2]에 dp[2]의 타일을 곱해준다.

-> dp[N] = dp[N-2] * dp[2]

2. N-4에서 2씩 계속 빼주면서 특별한 타일의 수를 곱해서 누적해 준다.

-> dp[N] += dp[N-4에서 2씩 감소] * 2; 

3. N일 때 특별한 타일 2개를 누적해서 더해준다. 

-> dp[N] += 2; 

 

전체코드

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();

        if (N % 2 != 0) {
            System.out.println(0);
            return;
        }

        int[] dp = new int[N + 1];

        dp[2] = 3;

        for(int i = 4; i <= N; i += 2) {
            dp[i] = dp[i-2] * dp[2];
            for(int j = i-4; j > 0; j-=2) {
                dp[i] += dp[j] * 2;
            }
            dp[i] += 2;
        }
        System.out.println(dp[N]);
    }
}

 

 

자신의 특별한 타일 2개를 dp[0]으로 계산해도 된다. 

dp[0]을 1로 초기화하고 2로 매번 곱해서 누적해 주면 2를 계속 더해주는 것과 같다.

 

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int N = sc.nextInt();

        if (N % 2 != 0) {
            System.out.println(0);
            return;
        }

        int[] dp = new int[N + 1];
        dp[0] = 1;
        dp[2] = 3;

        for(int i = 4; i <= N; i += 2) {
            dp[i] = dp[i-2] * dp[2];
            for(int j = i-4; j >= 0; j-=2) {
                dp[i] += dp[j] * 2;
            }
        }
        System.out.println(dp[N]);
    }
}

 

 

상세한 해설은 아래 블로그를 참고하자

https://yabmoons.tistory.com/536